Simulateur d’ordinateur quantique

Bonjour, en apprenant la base de la mécanique quantique, j’ai fais un détour sur l’ordinateur quantique. Pour bien assimiler le tout j’ai conçu un simulateur d’ordinateur quantique simple d’utilisation. Il permet de simuler facilement des graphes quantiques avec la plupart des portes et autant de qubits que l’on souhaite.

Avant toute chose, le lien du programme : https://github.com/FrancoisJ/Quantum_Computer.

Le programme est en python, mais il n’est pas nécessaire de connaître le langage, j’ai coder un mini interpréteur pour une utilisation plus simple. L’idée est de transcrire un graphe en script. Ensuite on vient exécuter le script.

Le programme a deux modes : le prompteur permet d’exécuter le code ligne par ligne directement par la commande ./computer, il permet aussi d’accéder à l’aide par la commande help. Le deuxième mode est la lecture d’un script par la commande ./computer le_fichier. Voyons quelques exemples d’algorithmes connus, que l’on peut simuler.

Exemples

Deutsch

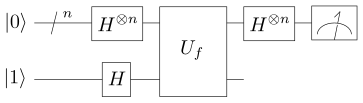
L’algorithme de Deutsch permet de savoir si un fonction renvoie toujours le même résultat ou non. Ce qui a de fort avec cet algorithme c’est qu’il permet de connaître le résultat en mesurant une seule fois la fonction. Une belle analogie serait de vérifier si une pièce est truquée, dans ce cas elle renvoie toujours la même valeur. Cet algorithme permet de vérifier la pièce en regardant que d’un seul coté, ceci grâce au propriété de la mécanique quantique.

Voici, la traduction du schémas pour mon programme, ici la fonction prend soit 0 ou 1, avec f(x) = x.

# This exemple implements the Deutsh algorithm

# Initialize computer variable
qubit x 1 0
qubit y 0 1
# Choose balanced or not function
function f
y = x
endfunction

# Perform some gates
hadamard [x,y]
uf f x y
hadamard x

# Make a measure
# if function is balanced, result will be 1
# then, result will be -1
measure x

Grover

L’algorithme de grover permet de retrouver un élément dans une base de donnée. Une porte nommée oracle viendra taguer l’élément que l’on souhaite et une série de porte viendra extraire l’élément. Un tel algorithme sur un ordinateur classique a une complexité de , avec celui de grover on obient .

Ci-dessous un schéma de l’algorithme avec 8 quibts + 1 quibt de resultat. On a donc une base de donnée de 256 éléments. Nous souhaitons extraire l’élément 57, la fonction oracle est .

Voici le script correspondant :

# add qubit x
qubit x1 1 0
qubit x2 1 0
qubit x3 1 0
qubit x4 1 0
qubit x5 1 0
qubit x6 1 0
qubit x7 1 0
qubit x8 1 0
# add qubit q
qubit q 0 1

# perform hadamard
hadamard [x1,x2,x3,x4,x5,x6,x7,x8,q]

# add oracle function
function o
if x==57 :
    y = 1
else :
    y = 0
endfunction


# iteration = pi/4*sqrt(2^n)
repeat 12
oracle o [x1,x2,x3,x4,x5,x6,x7,x8] q
hadamard [x1,x2,x3,x4,x5,x6,x7,x8]
s0 [x1,x2,x3,x4,x5,x6,x7,x8]
hadamard [x1,x2,x3,x4,x5,x6,x7,x8]
endrepeat

measure x1
measure x2
measure x3
measure x4
measure x5
measure x6
measure x7
measure x8

Fonctionnement

L’utilisation du logiciel est fini, pour plus de renseignements le logiciel dispose d’une aide. Lancer le prompteur par ./computer puis taper help. Je vais maintenant vous expliquer le fonctionnement.

Avant toute chose sachez qu’il est simple. Le fichier computer.py fait peut-être 1000 lignes, mais seulement 300 servent pour la simulation, le reste sert pour l’interpréteur et l’aide.

Prennons l’exemple d’une porte générique à un qubit :

Le problème avec la notation matricielle, c’est que le nombre de qubit doit être fixé à l’avance pour construire les matrices. On peut trouver une autre méthode de calcul moins contraignante et plus procédurale.

Si nous avons notre qubit X dans l’état : , alors

Tout cela peut se traduire d’une manière conditionnelle : Si , (), alors l’état devient et l’état devient . Si , (), alors l’état devient et l’état devient .

Lorsque l’état de l’ordinateur est intriqué, il suffit de suivre la démarche ci-dessus sur tous les sous-états. Prenons une exemple. L’ordinateur possède deux qubit , admettons que l’état intriqué de l’ordinateur donne

Nous souhaitons appliquer sur la porte de Hadamard

Soit

A> l’état avant la porte, et

B> l’état après. On va utiliser le choix conditionnel vu plus haut sur chaque sous-état. Pour le sous-état

00> de

A>: y est en

0>, on a donc sur l’état

00> de

B>, et pour l’état

01> de

B>. Ensuite les états

01> et

10> de

A> sont nuls, donc on ne fait rien. Enfin l’état

11> de

A> : y est en

1>, on a donc sur

10> de

B> et sur l’état

11> de

B>. Ce qui nous donne le nouvel état :

Au final, c’est un peu la technique que l’on fait avec un papier et un crayon quand on fait le calcul à la main. Je vous mets le bout de code gérant les portes logiques à un qubit, il y a quelques petites choses qui changent :

1. l’état intriqué est stocké dans un narray de numpy self.state, il faut donc tout le temps convertir les indices en décimal vers le binaire. J’utilise des tableaux de bits. Exemple : dec2bin(5) = [1, 0, 1], bin2dec([1, 1, 1]) = 7.
2. L’utilisateur différencie les qubits par des lettres. On a donc un dictionnaire self.names qui fait la traduction nom du qubit, emplacement dans le tableau binaire. Avec notre exemple, on a self.name = {'x' : 1, 'y': 0}.

new_state = np.zeros(len(self.state), dtype=complex)

for i in range(0, len(self.state)) :
    binary = self.dec2bin(i)


    if binary[ self.names[n] ] == 0 :
        new_state[i] += a*self.state[i]
        binary[ self.names[n] ] = 1
        new_state[ self.bin2dec(binary) ] += c*self.state[i]

    elif binary[ self.names[n] ] == 1 :
        new_state[i] += d*self.state[i]
        binary[ self.names[n] ] = 0
        new_state[ self.bin2dec(binary) ] += b*self.state[i]

self.state = new_state 

Le reste du programme repose sur ce procédé, et ne devrait pas poser de problème pour comprendre.